IMAT Physics Formula Compendium

This section lays the foundation for all physics topics by defining fundamental concepts related to measurement, units, and vector operations. A deep understanding of this area is essential, as problems involving unit conversions and formula manipulations are frequently encountered.

1.1 Basic and Derived Physical Quantities

Physics is built on accurately defined quantities, categorized into independent basic physical quantities (or base quantities) and derived physical quantities, which are expressed from basic quantities. In the International System of Units (SI), the following seven basic quantities form the foundation of measurement:

• Length: meter (m)
• Mass: kilogram (kg)
• Time: second (s)
• Electric Current: ampere (A)
• Thermodynamic Temperature: kelvin (K)
• Amount of Substance: mole (mol)
• Luminous Intensity: candela (cd)

From these basic units, many derived quantities are derived. For example, velocity is in meters per second (m/s), acceleration in meters per second squared (m/s²), force in newtons (N = kg·m/s²), pressure in pascals (Pa = N/m²), energy in joules (J = N·m), power in watts (W = J/s), charge in coulombs (C = s·A), and electrical resistance in ohms (Ω = V/A). Physical concepts are not isolated but form a coherent, interconnected framework. Understanding how derived units are expressed as combinations of basic units helps not just in memorizing units but in intuitively grasping their relationships. This understanding provides a deeper insight into the structure of physics and a powerful tool for self-checking the accuracy of formulas.

1.2 Systems of Units (SI)

The International System of Units (SI) is the globally recognized standard for scientific and technical measurement, ensuring consistency and comparability across different fields and regions. IMAT exam questions predominantly use SI units, making familiarity with them essential. SI prefixes are standardized multipliers used to express very large or small values concisely and clearly. For example, 1 kilometer (km) is equal to 10³ meters (m), and 1 microsecond (µs) is equal to 10⁻⁶ seconds (s). Prefixes range widely, from quetta (10³⁰) to quecto (10⁻³⁰). Scientific notation is the standard method for writing very large or small numbers that are inconvenient to write in decimal form. It is crucial for handling calculations involving such numbers. The format is a × 10ⁿ, where 'a' is typically a floating-point number between 1 and 10 (or 0 and 10), and 'n' is an integer exponent of 10.

1.3 Vector Operations

Vectors are physical quantities that have both magnitude and direction. In contrast, scalars are quantities with only magnitude. Examples of vectors in physics include displacement, velocity, acceleration, and force.

Vector Addition

There are two main graphical methods for adding vectors:

• Draw the first vector as an arrow.
• Place the tail of the second vector at the head of the first vector. If there are more than two vectors, repeat this process for each vector.
• Draw an arrow from the tail of the first vector to the head of the last vector. This is the resultant vector (or sum).
• Measure the magnitude of the resultant vector and its angle relative to a reference frame to determine its direction.

📸 Source/Description: Figure 1: This figure shows vector A and vector B being added head-to-tail. The resultant vector R extends from the starting point of the first vector to the endpoint of the last vector.

• Draw the two vectors to be added (e.g., P and Q) with their tails touching.
• Complete the parallelogram using these vectors as adjacent sides.
• The diagonal of the parallelogram drawn from the common tail represents the sum (resultant vector R) of the two vectors.
• Measure the magnitude of the resultant vector and its angle relative to a reference frame to determine its direction.

The magnitude of the resultant vector can be calculated using the formula:

Where P and Q are the magnitudes of the vectors, and is the angle between them. The direction of the resultant vector R (angle with respect to vector P) can be found using:

📸 Source/Description: Figure 2: This figure illustrates the Parallelogram method for vector addition. Both methods yield the same resultant vector R.

Special Cases:

• Parallel (Same Direction): When , the magnitude of the resultant vector is simply the sum of the magnitudes of the individual vectors: R = P + Q.
• Opposite Direction: When , the magnitude of the resultant vector is the absolute difference of the magnitudes of the individual vectors: R = |P - Q|.
• Perpendicular: When , the magnitude of the resultant vector is found using the Pythagorean theorem: .

Vector Subtraction

Subtracting vector B from vector A is the same as adding the negative of vector B (-B) to vector A. A negative vector is defined as a vector with the same magnitude as the original vector but in the opposite direction. Therefore, .

Multiplication of a Vector by a Scalar

Multiplying a vector by a scalar quantity c results in a new vector whose magnitude is the absolute value of c times the original magnitude. If the scalar c is positive, the direction of the vector remains unchanged. If the scalar c is negative, the direction of the vector is reversed.

Unit Conversion and Formula Manipulation

IMAT exams frequently feature problems requiring unit conversion and formula manipulation. This indicates the importance of not just memorizing formulas, but also understanding the relationships between physical quantities and the principles of dimensional analysis. Unit conversions are systematically handled by multiplying by a conversion factor equal to one, such that the desired unit replaces the original unit.

Common Unit Conversion Examples:

• To convert km/h to m/s, multiply by or the simplified fraction . Example: .
• 1 m = 100 cm
• 1 kg = 1000 g

This skill is essential for accurately solving physics problems. By carefully tracking units, you can ensure the accuracy of your calculations and maintain physical meaning.

Kinematics is the branch of physics that describes the motion of objects without considering the forces that cause the motion.

2.1 Parameters of Motion

Several basic parameters are used to describe the motion of an object:

• Displacement (s or x): The change in an object's position. It is a vector quantity.
• Velocity (v): The rate of change of displacement with respect to time. It is a vector quantity.
• Acceleration (a): The rate of change of velocity with respect to time. It is a vector quantity.
• Time (t): The duration over which motion occurs.

2.2 Uniform Rectilinear Motion

Uniform rectilinear motion is the motion of an object along a straight line at a constant velocity, which means the acceleration is zero.

Where is velocity, is displacement, and is the time interval. Example: A train traveling on a straight track at a constant speed.

2.3 Uniformly Accelerated Motion

Uniformly accelerated motion is the motion of an object with a constant acceleration. This means the object's velocity changes linearly with time. The key kinematic equations (SUVAT equations) are:

• Final Velocity:
• Displacement:
• Displacement (using average velocity):
• Final Velocity Squared:
• Displacement (using final velocity):

Where is initial velocity, is final velocity, is acceleration, is time, and is displacement. Examples include an object in free fall under gravity or a ball rolling down a frictionless ramp. It is crucial to follow a sign convention for direction when using these formulas.

2.4 Uniform Circular Motion

Uniform circular motion is the motion of an object in a circular path at a constant speed. While the speed is constant, the direction of the velocity is always changing, so the object is always accelerating. This acceleration is called centripetal acceleration and is always directed towards the center of the circle.

• Angular Velocity: , where T is the period.
• Tangential Velocity: , where r is the radius of the circle.
• Centripetal Acceleration: . This acceleration always points towards the center of the circle.
• Centripetal Force: . The net force, like the centripetal acceleration, always points towards the center of the circle.

Example: A racing car traveling at a constant tangential speed on a circular track.

📸 Source/Description: Figure 3: This diagram shows an object moving in a circular path, with a tangential velocity vector and a centripetal acceleration vector directed toward the center. The two vectors are always perpendicular.

2.5 Simple Harmonic Motion (SHM)

Simple Harmonic Motion is a type of periodic motion where the restoring force is directed towards the equilibrium position and is directly proportional to the displacement from that position.

Key Characteristics:

• Oscillatory Motion: The object moves back and forth over the same path.
• Restoring Force: The motion is always driven by a force directed towards an equilibrium position.
• Hooke's Law: Often described using the spring force: .
• Constant Period and Frequency: The time for each complete cycle of motion is constant.

Formulas:

• Displacement: or , where A is amplitude, ω is angular frequency, and φ is the phase constant.
• Velocity: (or ).
• Acceleration: . Acceleration is always opposite to displacement.
• Angular Frequency (mass-spring system): , where k is the spring constant and m is mass.
• Period:
• Frequency: .

Examples: a mass attached to a spring on a frictionless surface, a pendulum clock, the vibration of a tuning fork.

2.6 Motion Graphs (Position, Velocity, Acceleration vs. Time)

The motion of an object can be visually represented by graphs of position, velocity, and acceleration versus time. Understanding the relationship between these graphs is essential for analyzing motion.

Position-Time Graph:

• The value on the Y-axis represents position.
• The slope represents velocity.
• A constant positive slope indicates constant positive velocity (uniform motion).
• A changing slope (a curve) indicates changing velocity (accelerated motion).
• A horizontal line means the object is at rest (zero velocity).

Velocity-Time Graph:

• The value on the Y-axis represents velocity.
• The slope represents acceleration.
• A horizontal line indicates constant velocity (zero acceleration).
• A positive slope indicates positive acceleration (speeding up).
• A negative slope indicates negative acceleration (slowing down).
• The area under the curve represents displacement.

Acceleration-Time Graph:

• The value on the Y-axis represents acceleration.
• A horizontal line indicates constant acceleration.
• The area under the curve represents the change in velocity.

Graphs of SHM:

The graphs of displacement, velocity, and acceleration in SHM are all periodic functions (sine or cosine waves) and are 90° out of phase with each other. When displacement is maximum or minimum, velocity is zero. When displacement is zero (at the equilibrium position), velocity is maximum. Acceleration is always directed opposite to displacement and is maximum when displacement is maximum.

📸 Source/Description: Figure 4: This diagram shows how displacement, velocity, and acceleration change over time in simple harmonic motion. The graphs are periodic and have a 90-degree phase difference relative to each other.

Dynamics is the branch of physics that studies forces and how they affect the motion of objects.

3.1 Forces and Their Interactions (Newton's Laws)

Newton's laws of motion form the foundation of classical mechanics.

• First Law (Inertia): An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced external force. This law introduces the concept of inertia, the property of an object to resist changes in its state of motion.
• Second Law: The net force acting on an object is equal to the product of its mass and acceleration. This law also states that force is equal to the time rate of change of momentum.
• Third Law (Action-Reaction): For every action, there is an equal and opposite reaction. This means that if two objects interact, the force exerted by the first object on the second is equal in magnitude and opposite in direction to the force exerted by the second object on the first. This law is the basis for the law of conservation of momentum.

3.2 Examples of Forces

• Gravity (Weight): The gravitational force acting on an object near the Earth's surface. , where m is mass and g is the acceleration due to gravity (approx. 9.8 m/s²).
• Universal Gravitation: The attractive force between any two masses. , where G is the universal gravitational constant.
• Elastic Force (Hooke's Law): The restoring force exerted by an elastic object when it is deformed. , where k is the spring constant and x is the displacement from equilibrium.
• Friction: A force that resists the relative motion between two surfaces in contact. , where μ is the coefficient of friction and R is the normal force.
• Normal Force: The support force exerted by a surface on an object resting on it, acting perpendicular to the surface.

Free-Body Diagrams

Free-body diagrams are an essential tool for visualizing and analyzing all the external forces acting on an object. The object is represented as a single point, and the forces acting on it are drawn as vectors extending outwards from that point. This allows for a clear understanding of force balance and its effect on motion, even in complex situations.

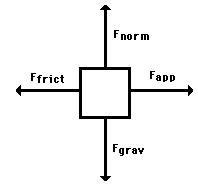
📸 Source/Description: Figure 5: This free-body diagram shows the two main external forces acting on a book on a table: the upward normal force (F_norm) from the table and the downward force of gravity (F_grav) from the Earth.

3.3 Moment of Force and Center of Mass

• Moment of Force (Torque): A measure of the tendency of a force to cause or change the rotational motion of an object. , where F is the force, r is the moment arm (distance from the axis of rotation to the line of action of the force), and θ is the angle between the force vector and the moment arm. If the force acts perpendicularly, the formula simplifies to M = Fr.
• Moment of a Couple: The torque produced by two parallel forces that are equal in magnitude, opposite in direction, and not on the same line of action. , where F is the magnitude of one of the forces and d is the perpendicular distance between their lines of action.
• Condition for Rotational Equilibrium: For an object not to rotate, the sum of all torques acting on it must be zero: or .
• Center of Mass of a System of Particles: The position of the center of mass is the weighted average of the positions of the individual parts.

3.4 Impulse and Momentum

Momentum is the product of an object's mass and velocity. Impulse is the change in momentum.

• Momentum (p): A vector quantity given by , where m is mass and v is velocity.
• Impulse (I): The product of the force and the time over which it acts. Impulse is equal to the change in momentum.
• Impulse-Momentum Theorem: .
• Conservation of Momentum: In an isolated system (where the net external force is zero), the total momentum remains constant. This principle is particularly important in scenarios like collisions and explosions.

3.5 Work, Energy, and Power

Work is done when a force causes a displacement. Energy is the capacity to do work. Power is the rate at which work is done.

• Work (W): Done when a force causes a displacement. , where F is force, d is displacement, and θ is the angle between them. The unit is the Joule (J).
• Kinetic Energy (KE): The energy an object possesses due to its motion. .
• Gravitational Potential Energy (GPE): Energy related to an object's position in a gravitational field. .
• Work-Energy Theorem: The net work done on an object equals the change in its kinetic energy (). Positive work increases kinetic energy, while negative work decreases it.
• Power (P): The rate at which work is done or energy is transferred. . The SI unit of power is the Watt (W), where 1 W = 1 J/s. In electrical systems: .

Conservation of Mechanical Energy: If only conservative forces (like gravity) act, the total mechanical energy (KE + PE) of a system is conserved. .

Fluid mechanics is the branch of physics that studies the properties and behavior of fluids (liquids and gases).

4.1 Fluid Properties and Behavior

• Fluid: A state of matter that yields to transverse or shear forces. Both liquids and gases are fluids.
• Density (ρ): Mass per unit volume. .
• Specific Gravity (s): The ratio of the density of a substance to the density of a reference substance, usually water. .

4.2 Hydrostatics (Fluids at Rest)

• Pressure (P): Force per unit area. . The SI unit is the Pascal (Pa).
• Pascal's Principle: A change in pressure applied to an enclosed, incompressible fluid is transmitted undiminished to every portion of the fluid and to the walls of the containing vessel. . Application: Hydraulic presses and car lifts.
• Stevin's Law (Hydrostatic Pressure): The pressure at a depth h in a fluid of constant density is given by . This law explains why pressure increases linearly with depth.
• Archimedes' Principle (Buoyant Force): The buoyant force on an object partially or fully immersed in a fluid is equal to the weight of the fluid that the object displaces. . This principle determines whether an object floats or sinks.

📸 Source/Description: Figure 6: This diagram shows a hydraulic system where Pascal's principle is applied. A force applied to a small piston is transmitted through the fluid, resulting in a larger amplified force on the larger piston.

📸 Source/Description: Figure 7: This diagram illustrates the concept of Archimedes' principle. An object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces.

4.3 Fluid Dynamics (Fluids in Motion)

• Flow Rate (Q): The volume of fluid passing a certain point per unit time. .
• Continuity Equation: For an incompressible fluid, the mass flowing into a pipe must equal the mass flowing out. This is based on the principle that fluid cannot be created or destroyed as it flows. . Application: The speed of water increases when the nozzle of a garden hose is narrowed.
• Bernoulli's Equation: An application of the law of conservation of energy for an ideal fluid (non-viscous and incompressible). . This equation implies that as the speed of a fluid increases, its pressure decreases, and vice versa. Application: Explains how aircraft wings generate lift and the Venturi effect.

Thermodynamics is the branch of physics that deals with heat, work, and temperature, and their relation to energy.

5.1 Equilibrium, Temperature, and Heat Transfer

Thermal Equilibrium: When objects at different temperatures are in contact, heat flows from the hotter object to the colder one until they reach the same temperature. This state is thermal equilibrium.

Modes of Heat Transfer: Heat is primarily transferred in three ways:

• Conduction: The process of heat transfer from a hotter part to a colder part of a substance without any actual movement of the molecules of the substance. Heat is transferred from molecule to molecule as a result of their vibrational motion. This generally occurs in solids.
• Convection: The process of heat transfer in liquids and gases from a region of higher temperature to a region of lower temperature. This occurs partly due to the actual movement of molecules, i.e., mass transfer.
• Radiation: The process of heat transfer from one body to another without involving the molecules of the medium. Heat transfer by radiation does not depend on a medium.

📸 Source/Description: Figure 8: This diagram shows the three main modes by which heat is transferred between objects or through a medium: conduction, convection, and radiation.

5.2 Heat Capacity and Specific Heat

Heat Capacity (C): The amount of heat energy required to raise the temperature of an object by one degree. . Heat capacity depends on the mass and composition of the object.

Specific Heat Capacity (c): The amount of heat energy required to raise the temperature of a unit mass of a substance by one degree. It is an intrinsic property of the substance and does not depend on its mass. The heat required to change the temperature of a substance is given by:

5.3 Phase Change and Latent Heat

Substances can change between different states (solid, liquid, gas) by absorbing or releasing heat. During this phase change, the temperature remains constant, and the heat absorbed or released is called latent heat. The heat required for a phase change at a constant temperature is:

Where L is a constant specific to the substance, known as the latent heat of fusion () or latent heat of vaporization ().

5.4 Ideal Gas Law

The ideal gas law is an equation of state that describes the relationship between the pressure, volume, temperature, and amount of a gas.

Where P is absolute pressure, V is volume, n is the number of moles, R is the ideal gas constant, T is absolute temperature (in Kelvin), N is the total number of atoms or molecules, and k is the Boltzmann constant.

5.5 Laws of Thermodynamics

• First Law: A statement of the conservation of energy. It states that energy cannot be created or destroyed, only transformed from one form to another or transferred from one system to another. The change in internal energy of a system equals the heat added to the system minus the work done by the system ().
• Second Law: This law has several expressions, but it generally states that heat spontaneously flows from a hotter body to a colder one, and that the entropy (degree of disorder) of an isolated system always increases or remains constant over time. This implies that heat engines have a limited efficiency and must always exhaust some heat to a colder reservoir.

A wave is a disturbance that transfers energy through a medium without any net movement of the medium itself.

6.1 Wave Characteristics

• Frequency (f) and Period (T): Frequency is the number of vibrations per unit time, and period is the time taken for one complete vibration. or . The SI unit for frequency is Hertz (Hz).
• Wave Speed (v): The speed at which a wave propagates through a medium, equal to the product of its frequency and wavelength. , where λ is the wavelength.

6.2 Sound Waves and Doppler Effect

• Speed of Sound (V): The speed of sound in air depends on the temperature: , where t is the temperature in degrees Celsius.
• Doppler Effect: The phenomenon where the observed frequency of a sound changes due to the relative motion between the sound source and the observer.
• Source moving towards observer:
• Source moving away from observer:

Where is the observed frequency, is the original frequency of the source, is the speed of sound, and is the speed of the source.

6.3 Law of Refraction

• Snell's Law: Describes the relationship between the angle of incidence and the angle of refraction when a wave passes through the boundary between two different media.
• Where is the angle of incidence, is the angle of refraction, are the wave speeds in each medium, are the wavelengths, and is the refractive index from medium 1 to medium 2.

Electricity and electromagnetism is the branch of physics that studies electric charges, electric fields, currents, magnetic fields, and their interactions.

7.1 Charge, Electric Field, and Potential

• Charge: A fundamental property of matter that causes electromagnetic interactions.
• Coulomb's Law: States that the force between two point charges is proportional to the product of their charges and inversely proportional to the square of the distance between them. , where k is Coulomb's constant.
• Electric Field (E): Defined as the force that would be exerted on a unit positive charge at a specific point in space. .
• Electric Potential/Voltage (V): Defined as the work done per unit charge. . The SI unit is the Volt (V).
• Equipotential Surface: A surface in space where the electric potential is constant.

7.2 Capacitance and Capacitors

• Capacitance (C): The ability to store electric charge. .
• Dielectric Constant (): The ratio of the capacitance with a dielectric material to the capacitance in a vacuum. .
• Capacitors in Series: The total capacitance is the reciprocal of the sum of the reciprocals of individual capacitances. .
• Capacitors in Parallel: The total capacitance is the simple sum of the individual capacitances. .

7.3 Current, Resistance, and Ohm's Law

• Electric Current (I): The amount of charge flowing per unit time. . The SI unit is the Ampere (A).
• Resistance (R): The opposition to the flow of electric current.
• Resistivity (ρ): An intrinsic property of a material that indicates how strongly it resists electric current. Resistance is determined by resistivity, length, and cross-sectional area: .
• Ohm's Law: States that the current flowing through a conductor is directly proportional to the voltage across it and inversely proportional to the resistance. .

7.4 Resistors in Series and Parallel

• Resistors in Series: The total resistance is the simple sum of the individual resistances. .
• Resistors in Parallel: The total resistance is the reciprocal of the sum of the reciprocals of the individual resistances. .

7.5 Kirchhoff's Principles

• Kirchhoff's Current Law (KCL / First Law): States that the sum of currents entering any junction in a circuit is equal to the sum of currents leaving that junction. This is based on the conservation of charge.
• Kirchhoff's Voltage Law (KVL / Second Law): States that the algebraic sum of the potential changes around any closed circuit loop is zero. This is based on the conservation of energy.

7.6 Work, Power, and the Joule Effect

• Electric Power: Calculated by .
• Joule Effect (Joule Heating): The phenomenon where heat is generated by resistance when an electric current flows through a conductor. The heat energy produced is given by .

7.7 Magnetic Fields and Electromagnetic Induction

• Magnetic Force on a Pole: A magnetic pole placed in a magnetic field experiences a force. , where is magnetic pole strength and H is magnetic field strength.
• Magnetic Flux Density (B): , where μ is the permeability of the medium.
• Magnetic Field from a Straight Current: , where I is current and r is distance.
• Magnetic Field at the Center of a Circular Current: .
• Magnetic Field Inside a Solenoid: , where n is turns per unit length.
• Force on a Current in a Magnetic Field (Lorentz Force): The force on a charge moving in a magnetic field is .
• Electromagnetic Induction (Faraday's Law): The electromotive force (emf) induced in a closed circuit is equal to the negative of the time rate of change of the magnetic flux through the circuit. . Lenz's Law is represented by the negative sign, indicating the induced current opposes the change that caused it. Application: Electric generators.

Atomic physics is the field of physics that studies the structure, properties, and behavior of atoms and their nuclei.

8.1 Radioactive Decay

The number of radioactive nuclei decreases exponentially over time according to the half-life.

Here, N(t) is the number of remaining nuclei, N₀ is the initial number of nuclei, t is the elapsed time, and T is the half-life.

8.2 Mass-Energy Equivalence

Einstein's famous equation shows that mass and energy are interconvertible. This relationship plays a crucial role in nuclear reactions and particle physics.

Where E is energy, m is mass, and c is the speed of light in a vacuum.

Success in the IMAT Physics section requires mastering the fundamental formulas and concepts detailed in this report. Each area of physics is interconnected; for example, understanding vectors in kinematics is directly applicable to analyzing forces in dynamics and fields in electromagnetism. Recognizing the interrelationships between physical quantities and how they are constructed from base units enhances accuracy in problem-solving and fosters the flexibility to apply existing knowledge to new situations. Simply memorizing formulas is not enough; it is crucial to understand their derivation, scope of application, and the physical principles they represent to solve complex problems accurately. Regular review and application of these formulas to a variety of problems are recommended to strengthen both theoretical knowledge and practical problem-solving skills, which will cultivate the deep understanding and application abilities required for the IMAT Physics exam.